1. Setting up Python and Brian¶
To solve the exercises you need to install Python, Brian2 and the neurodynex package. The installation procedure we described here focuses on the tools we use in the classroom sessions at EPFL. For that reason we additionally set up a conda environment (which we call bmnn below) and install Jupyter .
1.1. Using miniconda¶
We offer anaconda packages for the most recent releases, which is the easiest way of running the exercises. (Alternatively you can clone the sources from github)
Head over to the miniconda download page and install miniconda (for Python 2.7 preferably).
Now execute the following commands to install the exercise package as well as Brian2 and some dependencies. Note: we create a conda environment called ‘bmnn’. You may want to change that name. In the last command we install Jupyter , a handy tool to create solution documents.
>> conda create --name bmnn python=2.7
>> source activate bmnn
>> conda install -c brian-team -c epfl-lcn neurodynex
>> conda install jupyter
If you need to update the exercise package, call:
>> source activate bmnn
>> conda update -c brian-team -c epfl-lcn neurodynex
You now have the tools you need to solve the python exercises. To get started, open a terminal, move to the folder where you want your code being stored and start a Jupyter notebook:
>> cd your_folder
>> source activate bmnn
>> jupyter notebook
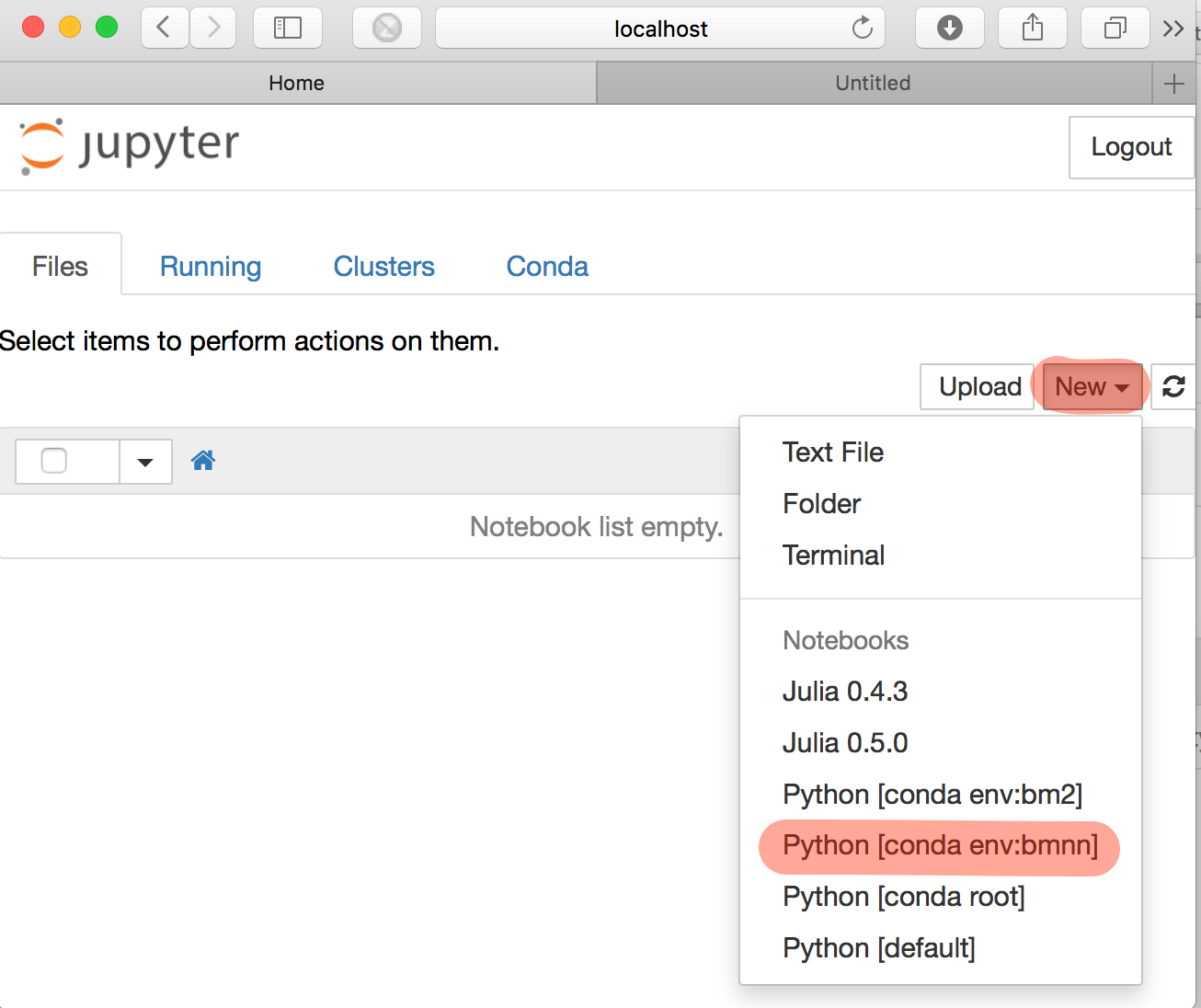
Starting Jupyter will open your browser. Select NEW, Python2 to get a new notebook page. Depending on what else you have installed on your computer, you may have to specify the kernel. In the case shown here, it’s the Python-bmnn installation.
We recommend you to create one notebook per exercise.
Note
Trouble shooting: You may get errors like ‘No module named ‘neurodynex’. This is the case when your jupyter notebook does not see the packages you’ve just installed. As a solution, try to re-install jupyter within the environment: .. code-block:
>> source activate bmnn
>> conda install jupyter
1.2. Links¶
Here are some useful links to get started with Python and Brian